Skip to main content

Computer Networking: IP Addressing and Subnetting

IP Addressing

Common Computer Numbering Systems

  • Binary (base 2) -- 0 to 1
  • Octal (base 8) -- 0 to 7
  • Decimal (base 10) -- 0 to 9
  • Hexadecimal (base 16) -- 0 to F 
BASE 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
--------------------------------------

When you see the number "4,529", you instinctively think...

   Four thousand five hundred and twenty-nine 
   (at least if you speak English anyway)

From birth, we as humans are taught to count in base 10
10 is a nice even number, working in multiples of 10 is easy


0 0 0 0                     4 5 2 9
| | | |___ 1                | | | |___    1 x 9 =    9
| | |_____ 10               | | |_____   10 x 2 =   20
| |_______ 100              | |_______  100 x 5 =  500
|_________ 1000             |_________ 1000 x 4 = 4000
                                                  ----
                                                  4529
BASE 2 (0, 1)
-------------

Computer chips use base 2 or binary because of the transistor
The transistor can either be in one of two states:

   - On  (1)
   - Off (0)

Processors can have billions of transistors
Allowing for computations of a massive range of values
Depending on the combinations of on/off states of transistors



0 0 0 0                  1 0 1 0
| | | |___ 1             | | | |___ 1 x 0 = 0
| | |_____ 2             | | |_____ 2 x 1 = 2
| |_______ 4             | |_______ 4 x 0 = 0
|_________ 8             |_________ 8 x 1 = 8
                                            ----
                                            10 (base 10)
                                            0A (base 16)
BASE 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B , C , D , E , F)
                                       10, 11, 12, 13, 14, 15  
-------------------------------------------------------------

Hexadecimal is widely used in computing, because:
    - It's more compact
    - Storing hexadecimal values consumes less resources
    - Converting between binary and hexadecimal is computationally easy


0 0 0 0                      F F E D
| | | |___ 1                 | | | |___    1 x 13 =    13
| | |_____ 16                | | |_____   16 x 14 =   224
| |_______ 256               | |_______  256 x 15 =  3840
|_________ 4096              |_________ 4096 x 15 = 61440
                                                    -----
                                                    65517 (base 10)

Decimal to Binary and Back Again

Binary to Decimal Conversion Examples 
CONVERT 0 BETWEEN DECIMAL AND BINARY
--------------------------------------
0   0  0  0  0  0  0  0
128 64 32 16 8  4  2  1
|   |  |  |  |  |  |  |_ 0 x 1 = 0 +
|   |  |  |  |  |  |
|   |  |  |  |  |  |_ 0 x 2    = 0 +
|   |  |  |  |  |
|   |  |  |  |  |_ 0 x 4       = 0 +
|   |  |  |  |
|   |  |  |  |_ 0 x 8          = 0 +
|   |  |  |
|   |  |  |_ 0 x 16            = 0 +
|   |  |
|   |  |_ 0 x 32               = 0 +
|   |
|   |_0 x 64                   = 0 +
|
|_ 0 x 128                     = 0
                                 ___
                                 0 (SUM)

CONVERT 255 BETWEEN DECIMAL AND BINARY
--------------------------------------
1   1  1  1  1  1  1  1
128 64 32 16 8  4  2  1
|   |  |  |  |  |  |  |_ 1 x 1 = 1  +
|   |  |  |  |  |  |
|   |  |  |  |  |  |_ 1 x 2    = 2  +
|   |  |  |  |  |
|   |  |  |  |  |_ 1 x 4       = 4  +
|   |  |  |  |
|   |  |  |  |_ 1 x 8          = 8  +
|   |  |  |
|   |  |  |_ 1 x 16            = 16 +
|   |  |
|   |  |_ 1 x 32               = 32 +
|   |
|   |_ 1 x 64                  = 64 +
|
|_ 1 x 128                     = 128
                                 ___
                                 255 (SUM)

You'll see that the sum of 8 bits is 255, which may lead you to wonder why you'll see a byte denoted as 256. This because in computing, 0 is also a possible binary value. If a byte can be denoted as 28, then we're calculating all the possible permutations of 8 bits -- including 0.

Effectively, if a byte is 8 bits, and if a bit can either be a 0 or a 1, then there are 256 possible values.

CONVERT 192 BETWEEN DECIMAL AND BINARY
--------------------------------------
1   1  0  0  0  0  0  0
128 64 32 16 8  4  2  1
|   |  |  |  |  |  |  |_ 0 x 1 = 0  +
|   |  |  |  |  |  |
|   |  |  |  |  |  |_ 0 x 2    = 0  +
|   |  |  |  |  |
|   |  |  |  |  |_ 0 x 4       = 0  +
|   |  |  |  |
|   |  |  |  |_ 0 x 8          = 0  +
|   |  |  |
|   |  |  |_ 0 x 16            = 0  +
|   |  |
|   |  |_ 0 x 32               = 0  +
|   |
|   |_ 1 x 64                  = 64 +
|
|_ 1 x 128                     = 128
                                 ___
                                 192 (SUM)
                                 
CONVERT 172 BETWEEN DECIMAL AND BINARY
--------------------------------------
1   0  1  0  1  1  0  0
128 64 32 16 8  4  2  1
|   |  |  |  |  |  |  |_ 0 x 1 = 0  +
|   |  |  |  |  |  |
|   |  |  |  |  |  |_ 0 x 2    = 0  +
|   |  |  |  |  |
|   |  |  |  |  |_ 1 x 4       = 4  +
|   |  |  |  |
|   |  |  |  |_ 1 x 8          = 8  +
|   |  |  |
|   |  |  |_ 0 x 16            = 0  +
|   |  |
|   |  |_ 1 x 32               = 32 +
|   |
|   |_ 0 x 64                  = 0  +
|
|_ 1 x 128                     = 128
                                 ___
                                 172 (SUM)

 

IP Addressing Formats

I am not going to get into any debates about why you should be using IPv6 versus IPv4. The majority of homes and business -- I imagine -- are still using IPv4 networks for their private addressing needs.

IPv4 depletion is a concern for public IPv4 addresses. There are some purists out there that like to make a lot of noise about it. However, if you prefer IPv4 addressing for use internally, that's perfectly fine.

  • An IP address -- in its simplest form -- is just a series of 1 and 0 bits (binary or base 2 numbering)
    • IPv4 is 32 bits -- thirty-two 1s and 0s
    • IPv6 is 128 bits -- one hundred and twenty eight 1s and 0s
  • We can take base 2 and convert to base 8, base 10, and base 16
    • Converting the IP address to decimal (base 10) makes it easier to store that information in databases
      • I've worked with a handful of security tools where the IP address was stored exclusively in decimal
    • Binary notation is too long, decimal is cleaner
  • The networking stack of the operating system can seamlessly work with multiple notations

IP Address Conversion Tool: https://www.hacksparrow.com/tools/converters/ip-address.html
More information here: https://www.hacksparrow.com/networking/many-faces-of-ip-address.html

Network Masking

An IP address is meaningless without a network mask. Given only an IP address, it is impossible to be certain which network this IP address is a member of. You may be able to infer, but you cannot be certain.

192      . 168      . 1        . 1 <-- IP Address
11000000 . 10101000 . 00000001 . 00000001

255      . 255      . 255      . 0 <-- Subnet Mask
11111111 . 11111111 . 11111111 . 0
  • Think of it like a zip code (or postal code)
    • A postal code confines residences to a specific area
    • A network mask confines hosts to a specific route
  • We also use network masks to determine the size of the network
  • The subnet mask is also -- in its simplest form -- just a series of 1 and 0 bits

No More Classful Networking

  • I don't like dwelling too much on the idea of Class A, Class B, or Class C networks
  • Those days are long gone. The world now operates on Classless Inter-Domain Routing (CIDR)
  • Instead, you should think of networks in terms of internet-routable and non-internet-routable
    • Public (WAN) / Private (LAN) / Diagnostic / Experimental / Reserved
    • RFC 1918 (non-internet-routable IPv4 addresses)
      • 10.0.0.0/8
      • 172.16.0.0/12
      • 192.168.0.0/16
    • RFC 4193 (non-internet-routable IPv6 addresses)
      • fc00::/7

More Information:
https://docs.netgate.com/pfsense/en/latest/network/addresses.html
https://en.wikipedia.org/wiki/Reserved_IP_addresses

Exploring Private IPv4 Network Masks

  • A network mask can be broken up into two parts
    • The network segment
    • The host segment
  • Private IPv4 Address Spaces
    • 10.0.0.0/8
      • Any host address between 10.0.0.1 and 10.255.255.254 is valid
    • 172.16.0.0/12
      • Any host address between 172.16.0.1 and 172.31.255.254 is valid
    • 192.168.0.0/16
      • Any host address between 192.168.0.1 and 192.168.255.254 is valid

The /8, /12, /16 are called CIDR notation or CIDR blocks. The number appearing after the slash ( / ) directly correlates to the sum of 1  bits in the binary notation of subnet mask. So /8 indicates that eight bits have been switched on.

10.0.0.0/8 
10       . 0-255    . 0-255    . 0-254
255      . 0        . 0        . 0        = /8
11111111 . 00000000 . 00000000 . 00000000 = 8 bits on (1 x 8)
    ^          ^          ^          ^
    |          |          |          |
 Network      Host       Host       Host
    |
    |
    |____ This octet is masked by 11111111
          Therefore, this octet is static at 10

 

172.16.0.0/12 
172      . 16-31    . 0-255    . 0-254
255      . 240      . 0        . 0        = /12
11111111 . 11110000 . 00000000 . 00000000 = 12 bits on (1 x 12)
    ^         ^^           ^          ^
    |         ||___________|          |
    |         |            |          |
 Network    Network      Host       Host
    |         |
    |         |
    |         |____ This octet is masked by 11110000
    |               Therefore, this octet has some variable range
    |
    |____ This octet is masked by 11111111
          Therefore, it is static at 172

This network is between /8 and /16 , which means that it was subnetted from a /8 network. So, we took a 172.16.0.0/8 and made it 172.16.0.0/12.  RFC 1918 has allocated one of 16 networks to be used as private, non-internet-routable address space.

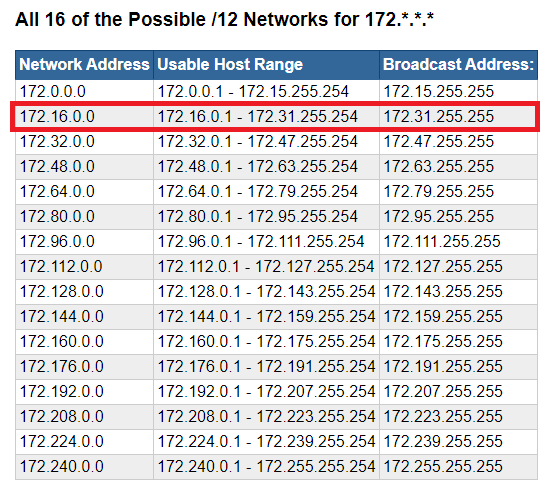image.png172.16.0.0/12 highlighted in red

This means that the remainder of networks in the 172.0.0.0/12 address space are internet-routable address blocks.

If you haven't noticed yet, the network address in the picture above increases in multiples of 16 -- 0, 16, 32, 48, 64, and so on. This is because our network mask is 11110000

 

Given a subnet mask, you can calculate the total number of possible networks the following ways:

  1. Find the partial network mask
    • A fully masked network ID is 8 bits -- 11111111
    • /8 , /16 , /24 , /32 represent CIDR masks where network ID octets are fully masked
      • 11111111.00000000.00000000.00000000 = /8
      • 11111111.11111111.00000000.00000000 = /16
      • 11111111.11111111.11111111.00000000 = /24
    • /12 is between /8 and /16
      • 11111111.11110000.00000000.0000000
             full          partial         host         host
  2. Then...
    • Use the decimal value of the network mask
    • Or, use the number of host bits as an exponent

Decimal Value

  • 11110000 (base 2) = 240 (base 10)
  • Total of 8 bits in a binary octet, with 256 possible values in decimal (as discussed earlier)
  • 256 - 240 = 16 

Host Bit Exponent

  • There are 4 bits in the host portion of the subnet mask
  • Binary is base 2, so 24 = 16
  • Again, 4 is the exponent here, as that's the number of host bits
  • The total possible values in binary, you'll recall, are 1 or 0, or base 2.
  • 24 = 16, hence the network ID increases in multiples of 16

172.0.x.x to 172.15.x.x -- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 -- 16 possible values (including zero)
172.16.x.x to 172.31.x.x -- 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 -- 16 possible values
Etc...

We'll get more practice with this a bit more down the page

Conversely, any octet where the network mask is 11111111 is fully masked, and the value can only be one value from 0 to 255

192.168.0.0/16

Technically speaking, if there's a 192.168.0.0/16 , there is a 192.0.0.0/8 , as demonstrated in the screenshot below.

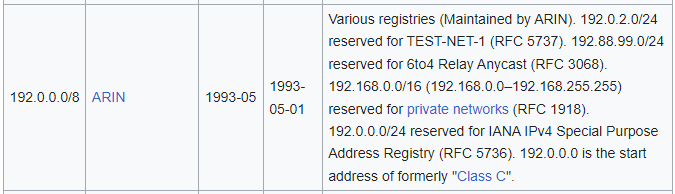image.pnghttps://en.wikipedia.org/wiki/List_of_assigned_/8_IPv4_address_blocks

Effectively, RFC 1918 has shrunk the /8 to /16 and said, that any address falling in 192.168.0.0/16 should be considered non-internet-routable (private).

192      . 168      . 0-255    . 0-254
255      . 255      . 0        . 0        = /16
11111111 . 11111111 . 00000000 . 00000000 = 16 bits on (1 x 16)
    ^          ^          ^          ^
    |          |          |          |
 Network     Network     Host       Host
    |          |
    |__________|
          |
          |
          |____ Both of these octets are masked by 11111111
                Therefore, both of these octets are static
                at 192 and 168 respectively

All of this is important, because every device with a network interface card (NIC) is going to have a routing table:

  • Hosts need to know what their Local Area Network (LAN) and what constitutes a foreign network
    • Can the host put the packet on the wire and let the switch take care of it?
    • Or, does it need to send it to the default gateway to be routed somewhere elese?
  • Routers need to be able to know how to move packets 

Subnetting

DON'T OVERTHINK IT!

Folks spend a lot of time upskilling in the HOW of subnetting, but I don't think training materials really spend enough time on the WHY of subnetting.

Why Do We Subnet?

A) To shrink the size of a network
B) To make multiple networks from a single network block

Scenario A: Shrink the 192.168.0.0/16 network

  • RFC 1918 has allocated the 192.168.0.0/16 address block for use in private computer networking
  • A /16 network will yield 65,534 possible addresses.
  • There's no way as residential users that we're going to use all of these addresses internally
192      . 168      . 0        . 0

255      . 255      . 0        . 0
11111111 . 11111111 . 00000000 . 00000000 = /16
   ^          ^           ^          ^
   |          |           |          |
Network    Network      Host        Host

Before

  • We can "borrow bits" from the host segment and switch them to 1 to make them a network segment
  • In this example, since we flipped all of the bits to 11111111, we can use any value between 0 and 255
  • We've add eight more bits to the network mask, making it a /24 network
  • 192.168.1.0/24 and 192.168.0.0/24 are very common subnets shipped on consumer-grade routers.
192      . 168      . 0-255    . 1-254

255      . 255      . 255      . 0
11111111 . 11111111 . 11111111 . 00000000 = /24
   ^          ^           ^          ^
   |          |           |          |
Network    Network     Network     Host
                          |          |
                          |          |______ This is the host octet now
                          |                  You can address any host from 1 through 254
                          |
                          |
                          |______ Choose a number between 0 through 255
                                  However, this now becomes part of the network ID
                                  So, this number is static, whichever you choose

After

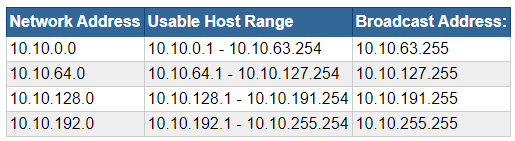
Scenario B: Increase the number of networks

Context

  • Think about this from a business perspective
  • You are working at an office branch and you are the network administrator
  • The network engineer at HQ gave you a 10.10.0.0/16 address space to work with
    • On its own, this address space yields:
      • 1 possible network
      • 65,534 possible hosts
    • You're required to work with this space and have no control over additional networks
    • You don't want to create routing conflicts with other branches in the organization
    • You control 10.10.0.0/16 and any subvariant of this address space

The Problem

  • You need to break this up into smaller chunks for multiple departments:
    • Sales
    • HR
    • Engineering
  • Once you've broken it up, you'll give this information to the network engineer, so that they can set up routes and firewall rules accordingly
10       . 10       . 0        . 0

255      . 255      . 0        . 0 
11111111 . 11111111 . 00000000 . 00000000 = /16
    ^          ^          ^          ^
    |          |          |          |
 Network    Network      Host       Host

The Solution

  • We know we need 3 networks
  • We need to calculate the number of host bits to borrow for the network mask.
  • The formula to check this is 2n, where n is the number of bits borrowed
    • 21 = 2, meaning 2 subnets are possible if we borrow 1 bit; not enough
    • 22 = 4, meaning 4 subnets are possible if we borrow 2 bits; more than we need, but the best possible choice
10       . 10       . 0         . 0

255      . 255      . 192       . 0 
11111111 . 11111111 . 110000000 . 00000000 = /18
    ^          ^          ^          ^
    |          |          |          |
 Network    Network      Host       Host

image.png

More Subnetting Practice

Shrink a Network Block

Scenario 1: Only 254 hosts per network

Problem

  • You're setting up a lab network and you've decided to use the 10.0.0.0/8 RFC 1918 spaces
  • In it's current state, you've got the following network mask
10       . 0        . 0        . 0

11111111 . 00000000 . 00000000 . 00000000
Network      Host       Host       Host

8  network bits
24 host bits
  • 224 = 16,777,216 = total addresses
  • (224) - 2 = 16,777,214 = total usable addresses (minus network and broadcast)
  • You don't need this many addresses in your lab environment

 

Calculate the Number of Usable Host Bits

  • (28) - 2 = 254 = total usable addresses = only 8 host bits
  • We know there's a total of 32 bits in the network mask
  • 32 total bits - 8 host bits = 24 = number of network bits
  • Yielding network mask of 11111111.11111111.11111111.00000000

Number of Usable Networks

10       . 0-255    . 0-255    . 1-254

11111111 . 11111111 . 11111111 . 00000000
Network  . Network  . Network  . Hosts
   |          |          |
   |          |          |____ Fully masked by 11111111
   |          |                Which ever decimal value we set it to is static
   |          |                Can choose any decimal value between 0-255
   |          |                This will be the network ID
   |          |
   |          |____ Fully masked by 11111111
   |                Which ever decimal value we set it to is static
   |                Can choose any decimal value between 0-255
   |                This will be the network ID
   |
   |____ Fully masked by 11111111
         This value cannot be anything other than 10
         The 10.0.0.0/8 network is the only "10" IP address block
         Reserved by RFC 1918 for private networking
  • 10 cannot be changed
  • The second octet is variable and open to our choosing -- 8 bits
  • The third octet is variable and open to our choosing -- 8 bits
  • 8 bits + 8 bits = 16 bits
  • 216 = 65,536 possible networks, with each network capable of having 254 hosts

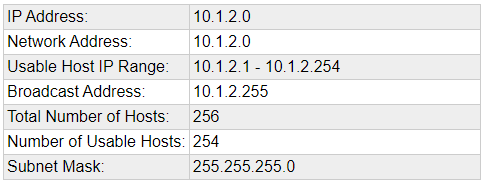
Example

10.1.2.0/24

10       . 1        . 2        . 1-254


255      . 255      . 255      . 0
11111111 . 11111111 . 11111111 . 00000000 = /24
Network    Network    Network    Hosts

10.1.2 - are the network ID and are static

The last octet can be any value between 1-254 as a usable address

image.png

Scenario 2: Only 30 hosts per network

Problem

  • You're setting up a lab network and you've decided to use the 172.16.0.0/12 RFC 1918 space
  • In it's current state, you've got the following network mask
172       . 16-31   . 0        . 0

11111111 . 11110000 . 00000000 . 00000000
Network    '-''---'    Host       Host       Host
           Net Host

12  network bits
20 host bits
  • 220 = 1,048,576 = total addresses
  • (220) - 2 = 1,048,574 = total usable addresses (minus network and broadcast)
  • You don't need this many addresses in your lab environment

Calculate the Number of Usable Host Bits

  • (25) - 2 = 30 = total usable addresses = only 5 host bits
  • We know there's a total of 32 bits in the network mask
  • 32 total bits - 5 host bits = 27 = number of network bits
  • Yielding network mask of 11111111.11111111.11111111.11100000

Number of Usable Networks

172      . 16-31    . 0-255    . 1-254

11111111 . 11111111 . 11111111 . 11100000
Network  . Network  . Network  . '-''---'
    |         |          |        |   |
    |         |          |       Net  Hosts
    |         |          |
    |         |          |____ Fully masked by 11111111
    |         |                Which ever decimal value we set it to is static
    |         |                Can choose any decimal value between 0-255
    |         |                This will be the network ID
    |         |
    |         |____ Per RFC 1918, this octet must be
    |               Any deciaml value of 16 through 31
    |
    |____ Per RFC 1918, this octet may only be 172
  • 172 cannot be changed
  • The second octet may be between 16 and 31 per RFC 1918
  • The third octet is variable and open to our choosing -- 8 bits
  • We've got a total of 27 bits in the network mask -- /27
  • The original network mask is 12 bits -- /12
  • 27 - 12 = 15
  • 215 = 32,768 possible networks, with each network capable of having 30 hosts

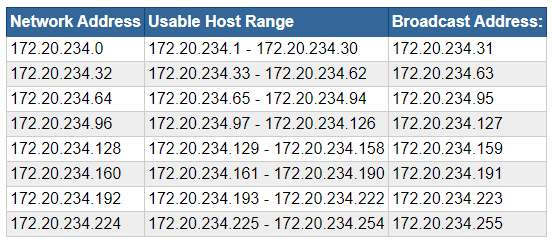
Example

172.20.234.0/27

image.png

Break up a Network Block

Scenario 1: Yield 3 Networks

Problem

  • You've been given a 192.168.1.0/24 network to work with
  • You need to divide this network up into three subnets

Convert the Subnet Mask to Binary

  • /24 means 24 bits are flipped on in the subnet mask
  • 11111111.11111111.11111111.00000000 (1 x 24 = 16)
     Network    Network   Network   Host

Calculate the Number of Host Bits to Borrow

  • 2n formula where n is the number of bits to borrow
  • 21 = 2 networks, which does not yield enough networks for us, as we need 4
  • 22 = 4 networks, which is more than we need, but the best we can do given the circumstances
Network Mask

255      . 255      . 255      . 192

11111111 . 11111111 . 11100000 . 11000000 = /26 (1 x 26)
 Network .  Network .  Network . --'----'
                                 ||   |
                             Network  Host
  • Our new CIDR notation is now /26 (1 x 26)
  • 192.168.1.0/26

Calculate the Network Size

  • 32 bits in a network mask
  • 32 - 26 = 6 host bits
  • 26 = 64 hosts per network

Calculate the Valid Decimal Values

192      . 168      . 1        . 0

255      . 255      . 255      . 192

11111111 . 11111111 . 11111111 . 11000000 = /26 (1 x 26)
 Network .  Network .  Network . --'----'
    |         |         |        ||   |
    |         |         |    Network  Host
    |         |         |             |
    |         |         |             |____ 6 host bits = 2^6 = 64 
    |         |         |                   64 total addresses per network
    |         |         |                   Increments of 64
    |         |         |
    |         |         |
    |         |         |____ Fully masked by 11111111
    |         |               This octet is static at
    |         |                   1
    |         |
    |         |_____ Fully masked by 11111111
    |                This octet is static at 
    |                    168
    |
    |____ Fully masked by 11111111
          This octet is static at
              192

 image.png

Note that the network ID address increases by increments of 64

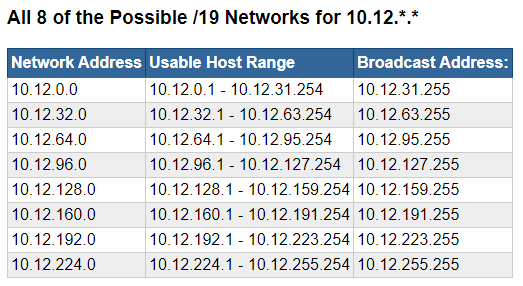
Scenario 2: Yield 8 Networks

Problem

  • You've been given a 10.12.0.0/16 network to work with
  • You need to divide this network up into eight subnets

Convert the Subnet Mask to Binary

  • /16 means 16 bits are flipped on in the subnet mask
  • 11111111.11111111.00000000.00000000 (1 x 16 = 16)
     Network    Network   Host         Host

Calculate the Number of Host Bits to Borrow

  • 2n formula where n is the number of bits to borrow
  • 23 = 8, therefore we need to borrow 3 bits from the host portion of the subnet mask
Network Mask

255      . 255      . 224      . 0

11111111 . 11111111 . 11100000 . 00000000 = /19 (1 x 19)
 Network .  Network . '-''---' . Host
                       |   |
                  Network  Host
  • Our new CIDR notation is now /19 (1 x 19)
  • 10.12.0.0/19

Calculate the Network Size

  • 32 bits in a network mask
  • 32 - 19 = 13 host bits
  • 213 = 8,192 hosts per network

Calculate the Valid Decimal Values

10       . 12       . 0        . 0

255      . 255      . 224      . 0

11111111 . 11111111 . 11100000 . 00000000 = /19 (1 x 19)
 Network .  Network . '-''---' . Host
                       |   |       |
                  Network  Host    |____ 8 host bits
                           |             2^8 = 0-255
                           |
                           |
                           |_____ 5 host bits
                                  2^5 = 0-31
                                  Increments of 32

image.png

Note that the network ID address increases by increments of 32

Back to top