Computer Networking: IP Addressing and Subnetting
IP Addressing
Common Computer Numbering Systems
- Binary (base 2) --
0to1 - Octal (base 8) --
0to7 - Decimal (base 10) --
0to9 - Hexadecimal (base 16) --
0toF
BASE 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
--------------------------------------
When you see the number "4,529", you instinctively think...
Four thousand five hundred and twenty-nine
(at least if you speak English anyway)
From birth, we as humans are taught to count in base 10
10 is a nice even number, working in multiples of 10 is easy
0 0 0 0 4 5 2 9
| | | |___ 1 | | | |___ 1 x 9 = 9
| | |_____ 10 | | |_____ 10 x 2 = 20
| |_______ 100 | |_______ 100 x 5 = 500
|_________ 1000 |_________ 1000 x 4 = 4000
----
4529BASE 2 (0, 1)
-------------
Computer chips use base 2 or binary because of the transistor
The transistor can either be in one of two states:
- On (1)
- Off (0)
Processors can have billions of transistors
Allowing for computations of a massive range of values
Depending on the combinations of on/off states of transistors
0 0 0 0 1 0 1 0
| | | |___ 1 | | | |___ 1 x 0 = 0
| | |_____ 2 | | |_____ 2 x 1 = 2
| |_______ 4 | |_______ 4 x 0 = 0
|_________ 8 |_________ 8 x 1 = 8
----
10 (base 10)
0A (base 16)BASE 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B , C , D , E , F)
10, 11, 12, 13, 14, 15
-------------------------------------------------------------
Hexadecimal is widely used in computing, because:
- It's more compact
- Storing hexadecimal values consumes less resources
- Converting between binary and hexadecimal is computationally easy
0 0 0 0 F F E D
| | | |___ 1 | | | |___ 1 x 13 = 13
| | |_____ 16 | | |_____ 16 x 14 = 224
| |_______ 256 | |_______ 256 x 15 = 3840
|_________ 4096 |_________ 4096 x 15 = 61440
-----
65517 (base 10)Decimal to Binary and Back Again
Binary to Decimal Conversion Examples
CONVERT 0 BETWEEN DECIMAL AND BINARY
--------------------------------------
0 0 0 0 0 0 0 0
128 64 32 16 8 4 2 1
| | | | | | | |_ 0 x 1 = 0 +
| | | | | | |
| | | | | | |_ 0 x 2 = 0 +
| | | | | |
| | | | | |_ 0 x 4 = 0 +
| | | | |
| | | | |_ 0 x 8 = 0 +
| | | |
| | | |_ 0 x 16 = 0 +
| | |
| | |_ 0 x 32 = 0 +
| |
| |_0 x 64 = 0 +
|
|_ 0 x 128 = 0
___
0 (SUM)
CONVERT 255 BETWEEN DECIMAL AND BINARY
--------------------------------------
1 1 1 1 1 1 1 1
128 64 32 16 8 4 2 1
| | | | | | | |_ 1 x 1 = 1 +
| | | | | | |
| | | | | | |_ 1 x 2 = 2 +
| | | | | |
| | | | | |_ 1 x 4 = 4 +
| | | | |
| | | | |_ 1 x 8 = 8 +
| | | |
| | | |_ 1 x 16 = 16 +
| | |
| | |_ 1 x 32 = 32 +
| |
| |_ 1 x 64 = 64 +
|
|_ 1 x 128 = 128
___
255 (SUM)You'll see that the sum of 8 bits is 255, which may lead you to wonder why you'll see a byte denoted as 256. This because in computing, 0 is also a possible binary value. If a byte can be denoted as 28, then we're calculating all the possible permutations of 8 bits -- including 0.
Effectively, if a byte is 8 bits, and if a bit can either be a 0 or a 1, then there are 256 possible values.
CONVERT 192 BETWEEN DECIMAL AND BINARY
--------------------------------------
1 1 0 0 0 0 0 0
128 64 32 16 8 4 2 1
| | | | | | | |_ 0 x 1 = 0 +
| | | | | | |
| | | | | | |_ 0 x 2 = 0 +
| | | | | |
| | | | | |_ 0 x 4 = 0 +
| | | | |
| | | | |_ 0 x 8 = 0 +
| | | |
| | | |_ 0 x 16 = 0 +
| | |
| | |_ 0 x 32 = 0 +
| |
| |_ 1 x 64 = 64 +
|
|_ 1 x 128 = 128
___
192 (SUM)
CONVERT 172 BETWEEN DECIMAL AND BINARY
--------------------------------------
1 0 1 0 1 1 0 0
128 64 32 16 8 4 2 1
| | | | | | | |_ 0 x 1 = 0 +
| | | | | | |
| | | | | | |_ 0 x 2 = 0 +
| | | | | |
| | | | | |_ 1 x 4 = 4 +
| | | | |
| | | | |_ 1 x 8 = 8 +
| | | |
| | | |_ 0 x 16 = 0 +
| | |
| | |_ 1 x 32 = 32 +
| |
| |_ 0 x 64 = 0 +
|
|_ 1 x 128 = 128
___
172 (SUM)
IP Addressing Formats
I am not going to get into any debates about why you should be using IPv6 versus IPv4. The majority of homes and business -- I imagine -- are still using IPv4 networks for their private addressing needs.
IPv4 depletion is a concern for public IPv4 addresses. There are some purists out there that like to make a lot of noise about it. However, if you prefer IPv4 addressing for use internally, that's perfectly fine.
- An IP address -- in its simplest form -- is just a series of
1and0bits (binary or base 2 numbering)
- IPv4 is 32 bits -- thirty-two 1s and 0s
- IPv6 is 128 bits -- one hundred and twenty eight 1s and 0s
- We can take base 2 and convert to base 8, base 10, and base 16
- Converting the IP address to decimal (base 10) makes it easier to store that information in databases
- I've worked with a handful of security tools where the IP address was stored exclusively in decimal
- Binary notation is too long, decimal is cleaner
- Converting the IP address to decimal (base 10) makes it easier to store that information in databases
- The networking stack of the operating system can seamlessly work with multiple notations
IP Address Conversion Tool: https://www.hacksparrow.com/tools/converters/ip-address.html
More information here: https://www.hacksparrow.com/networking/many-faces-of-ip-address.html
Network Masking
An IP address is meaningless without a network mask. Given only an IP address, it is impossible to be certain which network this IP address is a member of. You may be able to infer, but you cannot be certain.
192 . 168 . 1 . 1 <-- IP Address
11000000 . 10101000 . 00000001 . 00000001
255 . 255 . 255 . 0 <-- Subnet Mask
11111111 . 11111111 . 11111111 . 0- Think of it like a zip code (or postal code)
- A postal code confines residences to a specific area
- A network mask confines hosts to a specific route
- We also use network masks to determine the size of the network
- The subnet mask is also -- in its simplest form -- just a series of
1and0bits
No More Classful Networking
- I don't like dwelling too much on the idea of Class A, Class B, or Class C networks
- Those days are long gone. The world now operates on Classless Inter-Domain Routing (CIDR)
- Instead, you should think of networks in terms of internet-routable and non-internet-routable
- Public (WAN) / Private (LAN) / Diagnostic / Experimental / Reserved
- RFC 1918 (non-internet-routable IPv4 addresses)
10.0.0.0/8172.16.0.0/12192.168.0.0/16
- RFC 4193 (non-internet-routable IPv6 addresses)
fc00::/7
More Information:
https://docs.netgate.com/pfsense/en/latest/network/addresses.html
https://en.wikipedia.org/wiki/Reserved_IP_addresses
Exploring Private IPv4 Network Masks
- A network mask can be broken up into two parts
- The network segment
- The host segment
- Private IPv4 Address Spaces
10.0.0.0/8- Any host address between
10.0.0.1and10.255.255.254is valid
- Any host address between
172.16.0.0/12- Any host address between
172.16.0.1and172.31.255.254is valid
- Any host address between
192.168.0.0/16- Any host address between
192.168.0.1and192.168.255.254is valid
- Any host address between
The /8, /12, /16 are called CIDR notation or CIDR blocks. The number appearing after the slash ( / ) directly correlates to the sum of 1 bits in the binary notation of subnet mask. So /8 indicates that eight bits have been switched on.
10.0.0.0/8
10 . 0-255 . 0-255 . 0-254
255 . 0 . 0 . 0 = /8
11111111 . 00000000 . 00000000 . 00000000 = 8 bits on (1 x 8)
^ ^ ^ ^
| | | |
Network Host Host Host
|
|
|____ This octet is masked by 11111111
Therefore, this octet is static at 10
172.16.0.0/12
172 . 16-31 . 0-255 . 0-254
255 . 240 . 0 . 0 = /12
11111111 . 11110000 . 00000000 . 00000000 = 12 bits on (1 x 12)
^ ^^ ^ ^
| ||___________| |
| | | |
Network Network Host Host
| |
| |
| |____ This octet is masked by 11110000
| Therefore, this octet has some variable range
|
|____ This octet is masked by 11111111
Therefore, it is static at 172This network is between /8 and /16 , which means that it was subnetted from a /8 network. So, we took a 172.16.0.0/8 and made it 172.16.0.0/12. RFC 1918 has allocated one of 16 networks to be used as private, non-internet-routable address space.
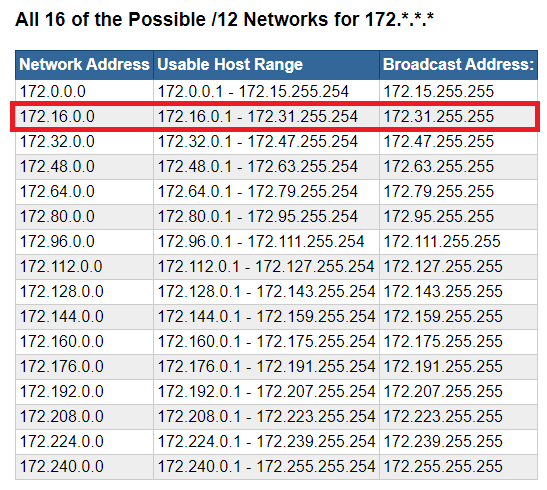 172.16.0.0/12 highlighted in red
172.16.0.0/12 highlighted in red
This means that the remainder of networks in the 172.0.0.0/12 address space are internet-routable address blocks.
If you haven't noticed yet, the network address in the picture above increases in multiples of 16 -- 0, 16, 32, 48, 64, and so on. This is because our network mask is 11110000
Given a subnet mask, you can calculate the total number of possible networks the following ways:
- Find the partial network mask
- A fully masked network ID is 8 bits --
11111111 /8,/16,/24,/32represent CIDR masks where network ID octets are fully masked11111111.00000000.00000000.00000000=/811111111.11111111.00000000.00000000=/1611111111.11111111.11111111.00000000=/24
/12is between/8and/1611111111.11110000.00000000.0000000
full partial host host
- A fully masked network ID is 8 bits --
- Then...
- Use the decimal value of the network mask
- Or, use the number of host bits as an exponent
Decimal Value
11110000(base 2) =240(base 10)- Total of 8 bits in a binary octet, with
256possible values in decimal (as discussed earlier) 256-240=16
Host Bit Exponent
- There are 4 bits in the host portion of the subnet mask
- Binary is base 2, so 24 = 16
- Again, 4 is the exponent here, as that's the number of host bits
- The total possible values in binary, you'll recall, are
1or0, or base 2. - 24 = 16, hence the network ID increases in multiples of 16
172.0.x.x to 172.15.x.x -- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 -- 16 possible values (including zero)172.16.x.x to 172.31.x.x -- 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 -- 16 possible values
Etc...
We'll get more practice with this a bit more down the page
Conversely, any octet where the network mask is 11111111 is fully masked, and the value can only be one value from 0 to 255
192.168.0.0/16
Technically speaking, if there's a 192.168.0.0/16 , there is a 192.0.0.0/8 , as demonstrated in the screenshot below.
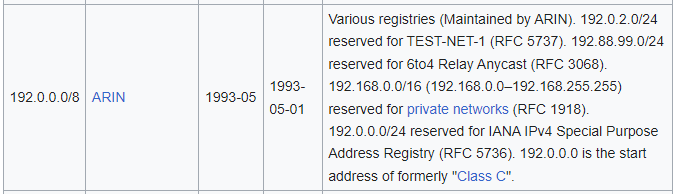 https://en.wikipedia.org/wiki/List_of_assigned_/8_IPv4_address_blocks
https://en.wikipedia.org/wiki/List_of_assigned_/8_IPv4_address_blocks
Effectively, RFC 1918 has shrunk the /8 to /16 and said, that any address falling in 192.168.0.0/16 should be considered non-internet-routable (private).
192 . 168 . 0-255 . 0-254
255 . 255 . 0 . 0 = /16
11111111 . 11111111 . 00000000 . 00000000 = 16 bits on (1 x 16)
^ ^ ^ ^
| | | |
Network Network Host Host
| |
|__________|
|
|
|____ Both of these octets are masked by 11111111
Therefore, both of these octets are static
at 192 and 168 respectivelyAll of this is important, because every device with a network interface card (NIC) is going to have a routing table:
- Hosts need to know what their Local Area Network (LAN) and what constitutes a foreign network
- Can the host put the packet on the wire and let the switch take care of it?
- Or, does it need to send it to the default gateway to be routed somewhere elese?
- Routers need to be able to know how to move packets
Subnetting
DON'T OVERTHINK IT!
Folks spend a lot of time upskilling in the HOW of subnetting, but I don't think training materials really spend enough time on the WHY of subnetting.
Why Do We Subnet?
A) To shrink the size of a network
B) To make multiple networks from a single network block
Scenario A: Shrink the 192.168.0.0/16 network
- RFC 1918 has allocated the
192.168.0.0/16address block for use in private computer networking - A
/16network will yield 65,534 possible addresses. - There's no way as residential users that we're going to use all of these addresses internally
192 . 168 . 0 . 0
255 . 255 . 0 . 0
11111111 . 11111111 . 00000000 . 00000000 = /16
^ ^ ^ ^
| | | |
Network Network Host Host
Before
- We can "borrow bits" from the host segment and switch them to
1to make them a network segment - In this example, since we flipped all of the bits to
11111111, we can use any value between0and255 - We've add eight more bits to the network mask, making it a
/24network 192.168.1.0/24and192.168.0.0/24are very common subnets shipped on consumer-grade routers.
192 . 168 . 0-255 . 1-254
255 . 255 . 255 . 0
11111111 . 11111111 . 11111111 . 00000000 = /24
^ ^ ^ ^
| | | |
Network Network Network Host
| |
| |______ This is the host octet now
| You can address any host from 1 through 254
|
|
|______ Choose a number between 0 through 255
However, this now becomes part of the network ID
So, this number is static, whichever you choose
After
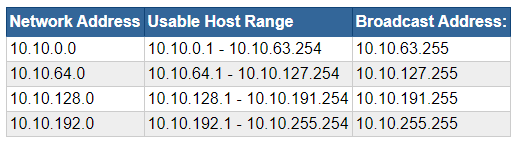
Scenario B: Increase the number of networks
Context
- Think about this from a business perspective
- You are working at an office branch and you are the network administrator
- The network engineer at HQ gave you a
10.10.0.0/16address space to work with- On its own, this address space yields:
- 1 possible network
- 65,534 possible hosts
- You're required to work with this space and have no control over additional networks
- You don't want to create routing conflicts with other branches in the organization
- You control
10.10.0.0/16and any subvariant of this address space
- On its own, this address space yields:
The Problem
- You need to break this up into smaller chunks for multiple departments:
- Sales
- HR
- Engineering
- Once you've broken it up, you'll give this information to the network engineer, so that they can set up routes and firewall rules accordingly
10 . 10 . 0 . 0
255 . 255 . 0 . 0
11111111 . 11111111 . 00000000 . 00000000 = /16
^ ^ ^ ^
| | | |
Network Network Host Host
The Solution
- We know we need 3 networks
- We need to calculate the number of host bits to borrow for the network mask.
- The formula to check this is 2n, where
nis the number of bits borrowed- 21 = 2, meaning 2 subnets are possible if we borrow 1 bit; not enough
- 22 = 4, meaning 4 subnets are possible if we borrow 2 bits; more than we need, but the best possible choice
10 . 10 . 0 . 0
255 . 255 . 192 . 0
11111111 . 11111111 . 110000000 . 00000000 = /18
^ ^ ^ ^
| | | |
Network Network Host Host
More Subnetting Practice
Shrink a Network Block
Scenario 1: Only 254 hosts per network
Problem
- You're setting up a lab network and you've decided to use the
10.0.0.0/8RFC 1918 spaces - In it's current state, you've got the following network mask
10 . 0 . 0 . 0
11111111 . 00000000 . 00000000 . 00000000
Network Host Host Host
8 network bits
24 host bits
- 224 = 16,777,216 = total addresses
- (224) - 2 = 16,777,214 = total usable addresses (minus network and broadcast)
- You don't need this many addresses in your lab environment
Calculate the Number of Usable Host Bits
- (28) - 2 = 254 = total usable addresses = only 8 host bits
- We know there's a total of 32 bits in the network mask
- 32 total bits - 8 host bits = 24 = number of network bits
- Yielding network mask of
11111111.11111111.11111111.00000000
Number of Usable Networks
10 . 0-255 . 0-255 . 1-254
11111111 . 11111111 . 11111111 . 00000000
Network . Network . Network . Hosts
| | |
| | |____ Fully masked by 11111111
| | Which ever decimal value we set it to is static
| | Can choose any decimal value between 0-255
| | This will be the network ID
| |
| |____ Fully masked by 11111111
| Which ever decimal value we set it to is static
| Can choose any decimal value between 0-255
| This will be the network ID
|
|____ Fully masked by 11111111
This value cannot be anything other than 10
The 10.0.0.0/8 network is the only "10" IP address block
Reserved by RFC 1918 for private networking10cannot be changed- The second octet is variable and open to our choosing -- 8 bits
- The third octet is variable and open to our choosing -- 8 bits
- 8 bits + 8 bits = 16 bits
- 216 = 65,536 possible networks, with each network capable of having 254 hosts
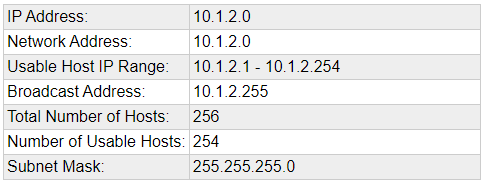
Example
10.1.2.0/24
10 . 1 . 2 . 1-254
255 . 255 . 255 . 0
11111111 . 11111111 . 11111111 . 00000000 = /24
Network Network Network Hosts
10.1.2 - are the network ID and are static
The last octet can be any value between 1-254 as a usable addressScenario 2: Only 30 hosts per network
Problem
- You're setting up a lab network and you've decided to use the
172.16.0.0/12RFC 1918 space - In it's current state, you've got the following network mask
172 . 16-31 . 0 . 0
11111111 . 11110000 . 00000000 . 00000000
Network '-''---' Host Host Host
Net Host
12 network bits
20 host bits
- 220 = 1,048,576 = total addresses
- (220) - 2 = 1,048,574 = total usable addresses (minus network and broadcast)
- You don't need this many addresses in your lab environment
Calculate the Number of Usable Host Bits
- (25) - 2 = 30 = total usable addresses = only 5 host bits
- We know there's a total of 32 bits in the network mask
- 32 total bits - 5 host bits = 27 = number of network bits
- Yielding network mask of
11111111.11111111.11111111.11100000
Number of Usable Networks
172 . 16-31 . 0-255 . 1-254
11111111 . 11111111 . 11111111 . 11100000
Network . Network . Network . '-''---'
| | | | |
| | | Net Hosts
| | |
| | |____ Fully masked by 11111111
| | Which ever decimal value we set it to is static
| | Can choose any decimal value between 0-255
| | This will be the network ID
| |
| |____ Per RFC 1918, this octet must be
| Any deciaml value of 16 through 31
|
|____ Per RFC 1918, this octet may only be 172172cannot be changed- The second octet may be between
16and31per RFC 1918 - The third octet is variable and open to our choosing -- 8 bits
- We've got a total of 27 bits in the network mask --
/27 - The original network mask is 12 bits --
/12 - 27 - 12 = 15
- 215 = 32,768 possible networks, with each network capable of having 30 hosts
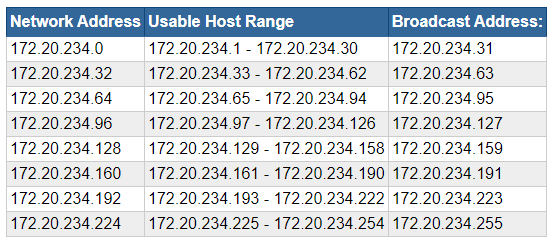
Example
172.20.234.0/27
Break up a Network Block
Scenario 1: Yield 3 Networks
Problem
- You've been given a
192.168.1.0/24network to work with - You need to divide this network up into three subnets
Convert the Subnet Mask to Binary
/24means 24 bits are flipped on in the subnet mask11111111.11111111.11111111.00000000(1 x 24 = 16)
Network Network Network Host
Calculate the Number of Host Bits to Borrow
- 2n formula where
nis the number of bits to borrow - 21 = 2 networks, which does not yield enough networks for us, as we need 4
- 22 = 4 networks, which is more than we need, but the best we can do given the circumstances
Network Mask
255 . 255 . 255 . 192
11111111 . 11111111 . 11100000 . 11000000 = /26 (1 x 26)
Network . Network . Network . --'----'
|| |
Network Host- Our new CIDR notation is now
/26(1 x 26) 192.168.1.0/26
Calculate the Network Size
- 32 bits in a network mask
- 32 - 26 = 6 host bits
- 26 = 64 hosts per network
Calculate the Valid Decimal Values
192 . 168 . 1 . 0
255 . 255 . 255 . 192
11111111 . 11111111 . 11111111 . 11000000 = /26 (1 x 26)
Network . Network . Network . --'----'
| | | || |
| | | Network Host
| | | |
| | | |____ 6 host bits = 2^6 = 64
| | | 64 total addresses per network
| | | Increments of 64
| | |
| | |
| | |____ Fully masked by 11111111
| | This octet is static at
| | 1
| |
| |_____ Fully masked by 11111111
| This octet is static at
| 168
|
|____ Fully masked by 11111111
This octet is static at
192Note that the network ID address increases by increments of 64
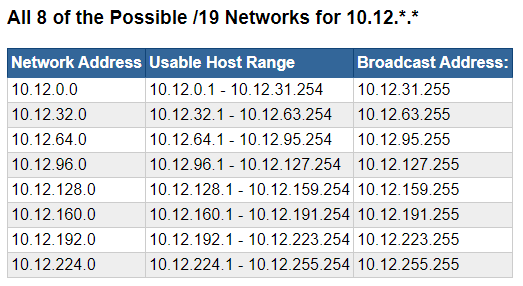
Scenario 2: Yield 8 Networks
Problem
- You've been given a
10.12.0.0/16network to work with - You need to divide this network up into eight subnets
Convert the Subnet Mask to Binary
/16means 16 bits are flipped on in the subnet mask11111111.11111111.00000000.00000000(1 x 16 = 16)
Network Network Host Host
Calculate the Number of Host Bits to Borrow
- 2n formula where
nis the number of bits to borrow - 23 = 8, therefore we need to borrow 3 bits from the host portion of the subnet mask
Network Mask
255 . 255 . 224 . 0
11111111 . 11111111 . 11100000 . 00000000 = /19 (1 x 19)
Network . Network . '-''---' . Host
| |
Network Host- Our new CIDR notation is now
/19(1 x 19) 10.12.0.0/19
Calculate the Network Size
- 32 bits in a network mask
- 32 - 19 = 13 host bits
- 213 = 8,192 hosts per network
Calculate the Valid Decimal Values
10 . 12 . 0 . 0
255 . 255 . 224 . 0
11111111 . 11111111 . 11100000 . 00000000 = /19 (1 x 19)
Network . Network . '-''---' . Host
| | |
Network Host |____ 8 host bits
| 2^8 = 0-255
|
|
|_____ 5 host bits
2^5 = 0-31
Increments of 32Note that the network ID address increases by increments of 32